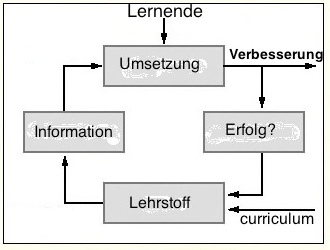
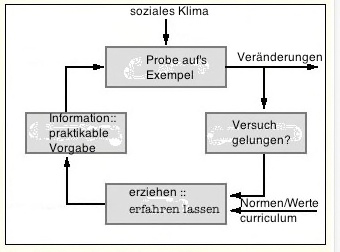
"Wir sind gewohnt, zu denken: Mathematik muss erst ”dagewesen“ sein, ehe sie in der Physik, in der Erdkunde, oder wo es auch sei, ”angewandt“ werden könne. Das ist die Haltung dessen, der sein Werkzeug bereitlegt, ehe er daran geht, Möbel zu bauen; logisch in Ordnung und vernünftig, besonders dann, wenn er Möbel ”in Serie“ herstellen will. Das führt zu Folgerungen wie dieser: Physik kann erst beginnen, ”wenn die nötigen mathematischen Voraussetzungen geschaffen sind“.
Was logisch richtig ist, kann aber auch pädagogisch blind oder doch unzureichend sein. Man muss erst wissen, was man in der Schule eigentlich will. Wirklich Kenntnisse in Serie herstellen? Vielleicht wird sich diese Vorstellung streckenweise nicht abweisen lassen. Aber pädagogisch wichtiger, oder mindestens komplementär dazu, erscheint ein anderer Grundsatz, der für den mathematischen Unterricht folgendes Ziel setzt: Erfahren lassen, wie Mathematik im ursprünglichen Umgang mit der Welt im Menschen entsteht, aus ihm also und aus den Dingen hervorgeht. Dann wird Mathematik nicht an-gewandt, sondern sie löst sich aus erdkundlichen, physikalischen, technischen und anderen Sachproblemen heraus und ist zugleich ein Mittel zu ihrer Bewältigung.
Wie tödlich langweilig ist es und allzu leicht zu verstehen, dass an zwei parallelen geraden Linien, die von einer dritten gekreuzt werden, Winkel sich finden lassen (mit schwer zu behaltenden Namen), die gleich groß sind. Langweilig, weil es ohne einen vernuünftigeren Anlass traktiert wird als aus der Gewohnheit, auf Vorrat zu stapeln, was dann später, irgendwann, unter tausend anderen solchen Dingen ”angewandt“ werden soll.
Wie anders aber sieht diese Figur aus, wenn sie aus einer unser Denken herausfordern- den Wirklichkeit herausgelesen wird: ursprünglich, indem sie uns die Antwort auf eine Frage zuspielt:
Eratosthenes (275 bis 195 v.Chr.) wollte herausbekommen, wie groß die Erdkugel ist. Er wusste schon, dass sie eine schwebende Kugel ist, damals, als niemand sie umfahren konnte, damals, als die denkende Mittelmeer-Welt der Antike sich wie eine kleine Lichtinsel von der riesigen Dunkelheit der unbekannten Länder und Völker umschlossen fühlte."
(aus: M. Wagenschein, ”Naturphänomene sehen und verstehen. Genetische Lehrgänge“, Klett: Stuttgart 1988, S. 298- 302.)
"Er weiß, dass oben in Ägypten, in Assuan (damals Syene) es vorkommt (an einem bestimmten Tage des Jahres, am 21. Juni), dass die Dinge keinen Schatten werfen; keinen seitlichen wenigstens; nur den kleinen, auf dem sie stehen, dem kleinsten. Und ein Obelisk (eine lange, nach oben sich verjüngende Pyramide) wirft also wirklich gar keinen. Er deckt die Stelle zu, auf die sein Schatten fallen sollte. Der Schatten liegt unter ihm bereit, und nachmittags wächst er seitlich heraus. Mittags hat er sich unter der Säule versteckt. Die Sonne steht zu Häupten, im ”Zenith“. Der Obelisk deutet auf sie.
Auch in Alexandria, im unteren Ägypten, annähernd nördlich von Syene, steht ein solcher Obelisk. Und, worauf es nun ankommt: im gleichen Augenblick, da die Säule in Assuan schattenlos dasteht, hat die in Alexandria einen deutlichen kleinen Schatten neben sich liegen!
Woher kommt das? Ist das nur so wie bei der Straßenlampe, die dem gar keinen Schatten macht, der genau unter ihr steht, einem anderen aber, ein paar Meter davon, sehr wohl?
Oder kommt es von dem, was Eratosthenes interessierte, daher nämlich, dass die beiden Säulen, wie Stacheln auf einem krummen Igelrücken, auf einer gewölbten Erde stehen? Eben weil die Erde als Ganzes eine Kugel ist. Wenn der eine Stachel auf die Sonne deutet, so tut es der andere schon nicht mehr. Je weiter er vom ersten weg ist, und je krummer (das heißt: kleiner) der Erdball ist, desto auffälliger wird das. – Oder trifft beides zusammen: Der Straßenlampen-Effekt (den es auch dann gäbe, wenn die Erde eine ebene Scheibe wäre) und der Igel-Effekt? Dann wäre die Frage leider kompliziert.
Nun ist das, was wir von der Lampe kennen, um so weniger auffällig, je höher sie über der Straße hängt. Und Eratosthenes und die Gelehrten seiner Zeit wussten damals schon, dass die Sonnenlampe so hoch über uns schwebt, so weit fort, dass der ganze große Erdball, mit diesem Abstand verglichen, fast ein Nichts ist.
Er wusste das nicht aus Büchern, wie wir Armen: er sah es. Wir können es auch sehen, und zwar am Mond (im ersten Viertel oder vorher), falls wir zugleich auf die Stellung der Sonne achten. (Es muss also Tag sein und beide Gestirne müssen am Himmel stehen). Dann sieht man, dass die Sonne viel weiter von uns abstehen muss als der Mond: Wenn man sich nämlich klarmacht, dass der Mond ein kalter, nur von der Sonne angeleuchteter Stein-Ball ist. (Das ist freilich schwer zu sehen; aber leicht, wenn man es einmal gesehen hat). Und da auch der Mond schon sehr weit ist (denn er ”geht immer mit“, hinter den Bergen, auch wenn wir sehr weit reisen), so ist die Sonne umso mehr fast unvorstellbar fern.
Das hier nur Angedeutete habe ich breiter dargestellt in: M. Wagenschein, ”Natur physikalisch gesehen“ 1953; jetzt Westermann, Braunschweig 1975; S. 59ff und in ”Die Erde unter den Sternen“, 3. Auflage Weinheim 1965, S. 22ff.)
Weil sie so fern sind, deshalb sind die beiden Sonnenstrahlen, die die Spitzen der beiden Obelisken treffen, – im Bereich unserer Figur so gut wie – gleichgerichtet (”parallel“). Damit wird alles einfach:
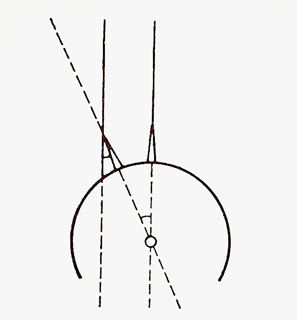
Es ist also nicht so wie bei der Straßenlampe, die über einer ebenen Straße hängt, es ist wie beim Igel nur die Krümmung des Erdbodens, die Krümmung Ägyptens, ist daran schuld, dass bei Alexandria ein Schatten hervorkommt. Die beiden Obelisken sind nicht parallel.
Mit zwei Streichhölzern, jedes in einem Plastillinsockel im Ägypten des Globus postiert, kann man sich das ganz klarmachen. Eine ferne helle Lampe als Sonne – oder auch die wirkliche Sonne selber – wirft den Schatten. Wenn man sich dann das ”worauf es an- kommt“, aus dem Globus heraus an die Tafel zeichnet, so löst sich aus diesem Bild hervor die Figur mit den zwei Parallelen und der dritten Geraden. Wohl dem, der sie noch nicht kennt.
Denn er kann dann die Entdeckung machen, dass der Winkel zwischen Assuan und Alexandria (genau: der Winkel zwischen den beiden Erdkugel-Radien, die auf die zwei Obelisken zeigen) – und das ist der Winkel, der uns interessiert, denn er zeigt ja die Krümmung an, wegen deren die alexandriner Säule gegen die von Assuan verdreht ist –, dass der Winkel, der tief in der Erde steckt, wohin wir nicht können, sich noch einmal wiederfindet an einem anderen Ort, und dort ganz zugänglich: an der Spitze des Obelisken in Alexandria: der Winkel zwischen der Spitze und dem seine Spitze streifenden Strahl, der die Spitze des Schattens auf den Boden malt. (Dass man nicht hinaufklettern braucht, um ihn zu messen, ist noch eine Entdeckung für sich). Anfangs ist es lustig, sich einen Ägypterknaben vorzustellen, der da oben, halb geblendet, den Winkel selbst in die Hände zu nehmen sucht. Haben wir diesen Winkel da oben gemessen, so zeigt sich die Mathematik sofort als Macht: Wir können ”schließen“ auf den anderen, ihm gleichen, der in der unzugänglichen Tiefe des Erdballes steckt, an einem Ort, an dem noch keiner war und wohl auch niemals ein Mensch sein wird und von dem niemand genau weiß, wie es dort ”aussieht“. Ist der Winkel, oben im Alexandria, am Obelisk, ein fünfzigstel Kreis – und so war es –, so ist es auch der in der Erde. Der Weg von Assuan nach Alexandria ist also ein Fünfzigstel des Weges um die ganze Erde herum, des Weges, den damals noch niemand gehen oder fahren konnte, und von dem keiner wusste, über wie viele Meere, durch welche Wüsten und was für fremde Völkerschaften er führen könnte. Aber wie weit dieser Weg sein musste, das wurde jetzt klar: Fünfzigmal die Strecke Alexandria-Assuan, und die konnte man messen: 5000 ”Stadien“, fast 1000 km. Aber auf die Zahl kommt es hier gar nicht so sehr an, ebenso wenig wie darauf, dass ein Fünfzigstel des vollen Winkels 7◦12 sind. Diese Zahlen, Einheiten und Zeichen verwirren nur. Es kommt hier nur auf eine Zahl an: Fünfzig; und darauf, dass man im Altertum von der Strecke Syene-Alexandria eine Vorstellung hatte.
Lernt man den Satz, dass jene zwei Winkel an Parallelen gleich sind, an der sterilen Figur, so lernt man fast gar nichts. Lernt man ihn aber gleich bei seiner Entdeckung aus einer Wirklichkeit herauslesen, so spürt man sofort etwas davon, was Mathematik ist und kann. (Nur etwas. Vom ”Beweisen“ ist noch gar keine Rede. Dazu ist der ”Satz“ zu selbstverständlich. Man braucht die Gleichheit der beiden Winkel nur zu vermuten und sagt schon ja dazu.) Man lernt das Abstrahieren, das Herausholen der Figur aus der Wirklichkeit. Die Wirklichkeit, das ist hier: die Weltinsel der Antike; die ägyptische hohe Sonne; die stillen Schatten im Mittagsglanz; das Tappen der Sohlen der Läufer, die damals die Strecke durchmessen mussten; der mitlaufende, also ferne Mond; die noch fernere, weil sichtlich hinter der Mondsichel sitzende Sonne. Aus dieser Wirklichkeit ziehen wir heraus, was damals wie heute gilt: Die unvergänglichen Denklinien der Geometrie, um eine Figur zu gewinnen, die zu einem abstrakten Reich gehört und uns doch die Macht gibt, die ganze Erde zu umspannen, ohne ein kleines Land zu verlassen."
(Ende Zitate N. Wagenschein)
Ein Grund für pädagogische Blindheit ist die Gewohnheit, die zu verhängnisvollen Vorurteilen führt wie beispielsweise, dass sich Mathematik nicht erfahren lässt. Nicht von ungefähr bedeutet das griechische Wort "Mathematik" "Technik des Lernens". Die griechischen Philosophen waren der Auffassung, dass Geometrie die trennschärfste Form des Lernens ist.
Um für das schöpferische Lernen offen zu sein können, muss man möglichst unvoreingenommen wahrnehmen. Das setzt eine positive Grundeinstellung voraus. Das folgende Beispiel zeigt, wie das unvoreingenommene Herangehen an eine Aufgabe durch Identifikationsversuche immer wieder gestört wird:
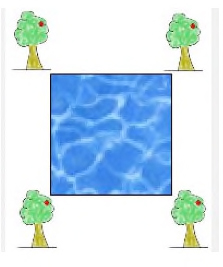
Ein Fischzüchter möchte seinen quadratischen Teich unter folgenden Bedingungen vergrößern:
Der Teich soll doppelt so groß wie bisher werden, ohne dass die vier schönen alten Bäume an dessen Ecken gefällt werden müssen und die quadratische Form verloren geht.
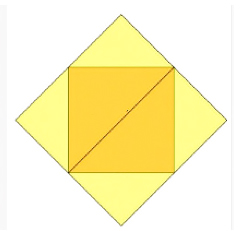
Es dauert eine Weile bis zur Idee, das Quadrat zu drehen und als Raute zwischen den Bäumen zu betrachten. Dass die Fläche der Raute doppelt so groß ist im Vergleich zur ursprünglichen Fläche des Quadrats, lässt sich leicht herausfinden, wenn die hellgelben Dreiecke auf das dunkelgelbe Quadrat nach innen geklappt werden.
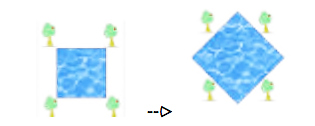
Theorie ist in diesem Fall die geometrische Begründung für die Verdopplung.

Eine Diagonale teilt ein Quadrat in zwei gleiche Dreiecke. Werden diese beiden Dreiecke zu einem rechtwinkligen Dreieck zusammengelegt, dann bilden sie die Hälfte eines doppelt so großen Quadrats.
Hintergrund bildet der Satz des Pythagoras: Nach diesem Satz bilden die beiden Quadrate über den Katheten a und b zusammen die gleiche Flächengröße wie das Quadrat über der Hypotenuse c.
Dieses Beispiel verdeutlicht, wie die mathematische Form bzw. Formel aus der Gestaltung heraus entsteht.